NeRF Revisited: Fixing Quadrature Instability in Volume Rendering
NeurIPS 2023
-
Mikaela Angelina Uy
Stanford University
-
George Kiyohiro Nakayama
Stanford University
-
Guandao Yang
Cornell University
Stanford University -
Rahul Krishna Thomas
Stanford University
-
Leonidas Guibas
Stanford University
-
Ke Li
Simon Fraser University
Google
Abstract
Neural radiance fields (NeRF) rely on volume rendering to synthesize novel views. Volume rendering requires evaluating an integral along each ray, which is numerically approximated with a finite sum that corresponds to the exact integral along the ray under piecewise constant volume density. As a consequence, the rendered result is unstable w.r.t. the choice of samples along the ray, a phenomenon that we dub quadrature instability. We propose a mathematically principled solution by reformulating the sample-based rendering equation so that it corresponds to the exact integral under piecewise linear volume density. This simultaneously resolves multiple issues: conflicts between samples along different rays, imprecise hierarchical sampling, and non-differentiability of quantiles of ray termination distances w.r.t. model parameters. We demonstrate several benefits over the classical sample-based rendering equation, such as sharper textures, better geometric reconstruction, and stronger depth supervision. Our proposed formulation can be also be used as a drop-in replacement to the volume rendering equation for existing methods like NeRFs.
Video
What We Are Were All Used To
One of the key underpinnings of the recent advances of coordinate-based representations, e.g. NeRFs, is volume rendering. Volume rendering enables end-to-end differentiable rendering, and hence has made learning of 3D geometry and appearance from only 2D images possible. In practice, the volume rendering integral is evaluated with quadrature resulting in the expressions shown below.
These expressions are what we've gotten used to, which is the exact integral under the piecewise constant assumption to opacity and color. However, this seemingly simple, innocuous assumption can result in the rendered image being sensitive to the choice of samples along the ray. While this does not necessarily cause a practical issue in classical rendering pipelines, it has surprising consequences when used in neural rendering.
PL-NeRF
We show that the piecewise constant assumption to opacity causes sensitivity to the choice of samples at both rendering and sampling time, which we dub as quadrature instability. This can lead to a number of issues: i) conflicting ray supervision leading to fuzzy surfaces, ii) imprecise samples and iii) lack of supervision on the CDF from samples.
Volume Rendering with Piecewise Linear Opacity
We revisit the quadrature used to approximate volume rendering in NeRF and devise a different quadrature formula based on a different approximation to the opacity. We derive the rendering equation under piecewise linear opacity and show that it both resolves quadrature instability and has good numerical conditioning.
We show that it has a simple and intuitive form and results in a new quadrature method for volume rendering, which can serve as a drop-in replacement for existing methods like NeRFs. We demonstrate that this reduces artifacts, improves rendering quality and results in better geometric reconstruction.
We also devise a new way to sample directly from the distribution of samples along each ray induced by NeRF without going through the surrogate, which opens the way to a more refined importance sampling approach and a more effective method to supervise samples using depth.
NeRF Results
We highlight the comparative advantage of PL-NeRF (linear) over Vanilla NeRF (constant) through a zoomed-in render of the side of a microphone.
In the constant model, conflicts in ray supervision between perpendicular and grazing angle rays result in fuzzier surfaces .
PL-NeRF alleviates this issue and yields a crisper textures on the microphone.


We also show qualitative video results from Blender scenes, which illustrate the improvements of the linear model over the constant model at various rendered camera views.
.gif)
.gif)
Chair: When the camera is positioned close to the chair, the slider shows sharper texturing on the chair patterns for the linear model than the constant model.
.gif)
.gif)
Microphone: At a bird's eye view, the linear model captures the internal structure of the microphone, which is lost in constant volume rendering.
Multidistance Results
We further consider the challenging setting of training with cameras at different distances to the object.
This results in different sets of ray samples leading to quadrature instability in the constant model.
PL-NeRF results in better renderings on multi-distance views: at all distances, the rendered outputs for PL-NeRF have sharper texture than Vanilla NeRF.
Furthermore, in Vanilla NeRF the level of noise (gold specs) and blurriness vary at different camera distances, whereas our PL-NeRF renders crisper and more consistent outputs over all distances.
1x Camera-to-Scene Distance:


0.5x Camera-to-Scene Distance:


0.25x Camera-to-Scene Distance:


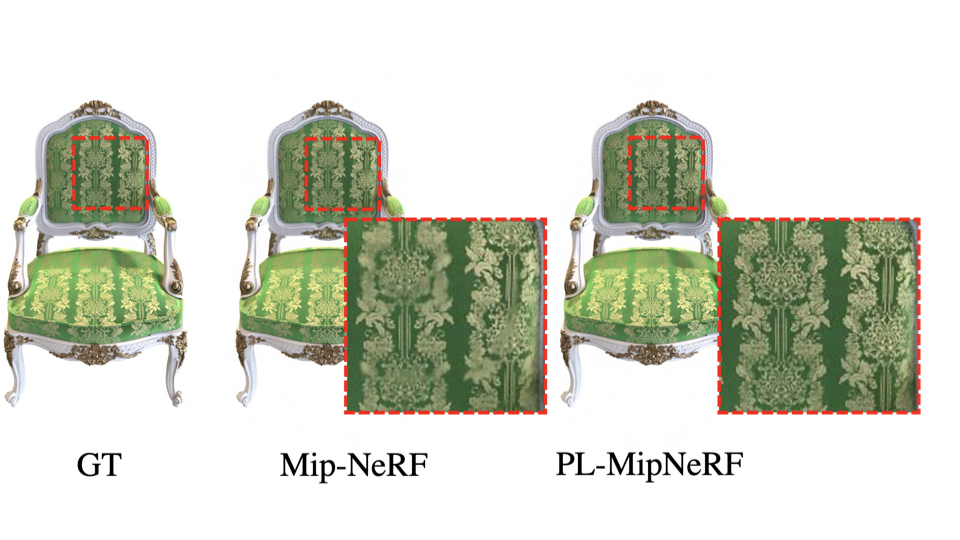
Mip-NeRF Results
We also integrate our piecewise linear opacity formulation into Mip-NeRF, which we call PL-MipNeRF.
We see that under difficult scenarios such as when ray conflicts arise in the fine texture details of the Chair and in the presence of grazing angle views in the Mic, our PL-MipNeRF shows significant improvement over the baseline.
This shows that our approach can be used as a drop-in replacement to existing NeRF variants.

Geometric Extraction
PL-NeRF also improves geometric reconstruction on coordinate-based networks. We can extract the geometry of a scene from the learned density field in the trained models of PL-NeRF and Vanilla NeRF. Below we show qualitative improvements in the reconstruction from the piecewise linear model, compared to the original piecewise constant formulation.
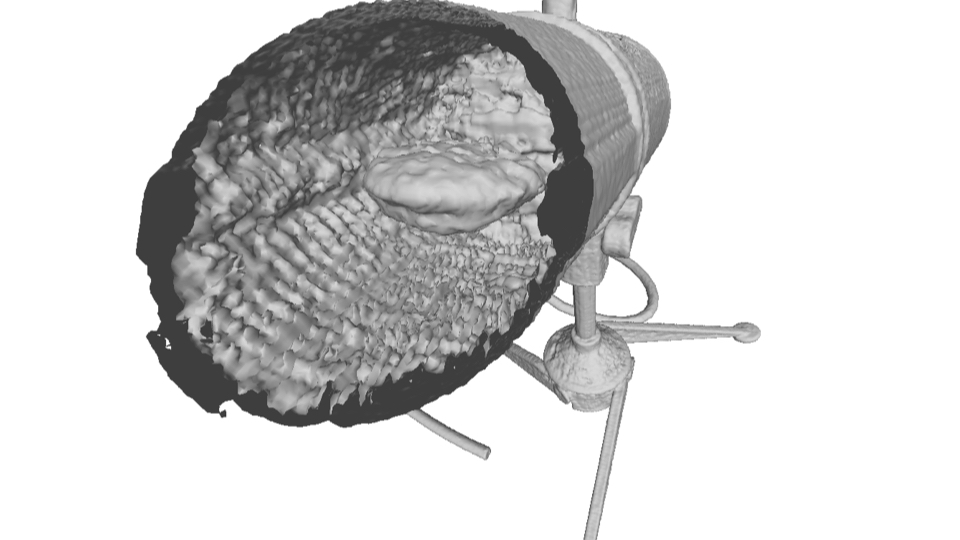
Microphone: PL-NeRF is able to better recover the structure inside the Mic, which is lost in the constant model.

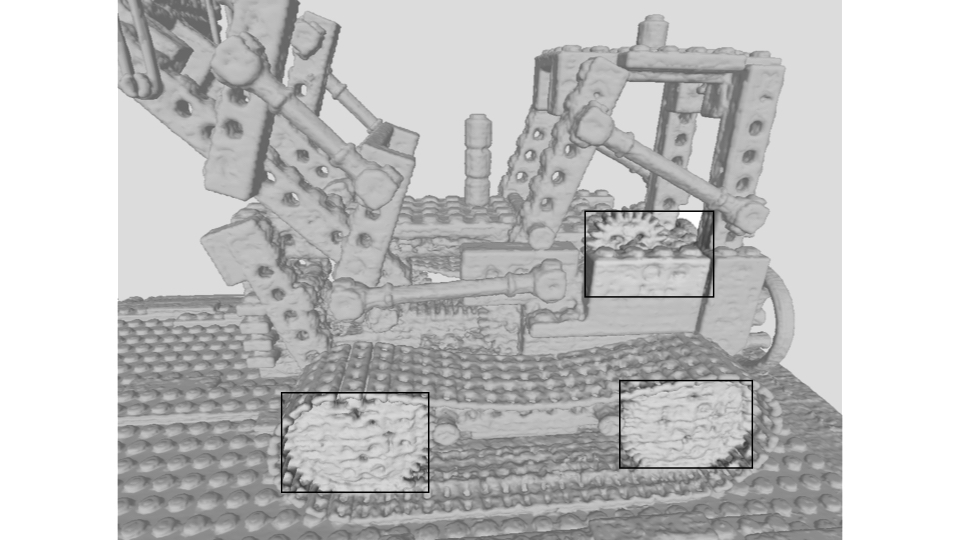
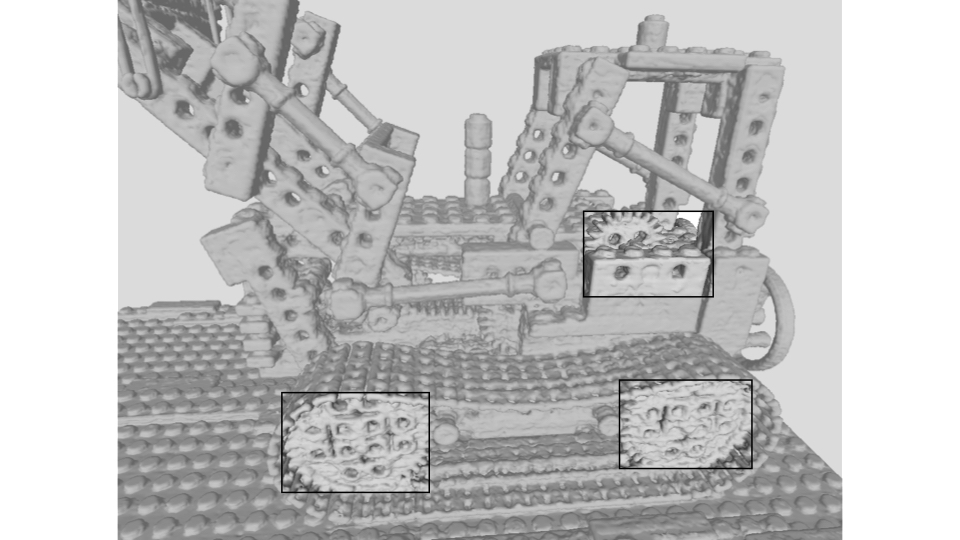
Lego: The holes on the body and wheels of the Lego scene become visually clearer in PL-NeRF.
Drums: Interestingly, the interior of a hollow drum is reconstructed as hollow in PL-NeRF.
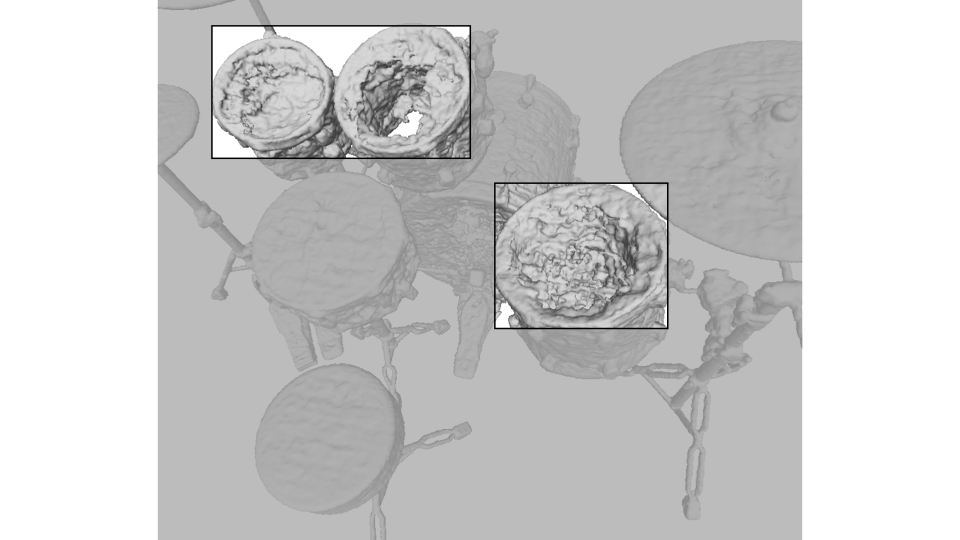
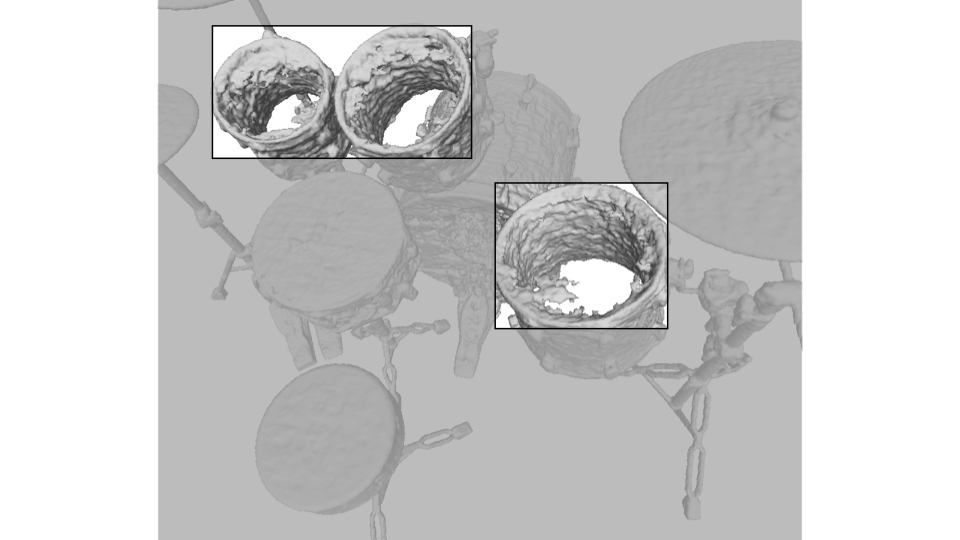
Even if the ground truth mesh is solid at the drum surface, PL-NeRF visually matches the image of the transparent drum (i.e. the only
signal used in supervised learning) better than NeRF, as shown below.

Citation
Acknowledgements
This work is supported by a Apple Scholars in AI/ML PhD Fellowship, a Snap Research Fellowship, a Vannevar Bush Faculty Fellowship, ARL grant W911NF-21-2-0104, a gift from the Adobe corporation, the Natural Sciences and Engineering Research Council of Canada (NSERC), the BC DRI Group and the Digital Research Alliance of Canada.
The website template was borrowed from BakedSDF.